Due to the complexity and the unknown dynamic model of the problem (see graph in Project description), the usual strategies of identifying causal estimands aren’t easy or obviously useful. Instead, I will be learning about a data analysis method to show linear dynamic modes in a non-linear system. The method is called Dynamic Mode Decomposition, or DMD.
Note: the notations used on this page is not consistent with those used in class.
The fundamental concept of DMD is to find the best-fit matrix, A, that predicts a quantity 
at time 
from measured quantity 
at 
. Suppose, there’s an unknown dynamic system with a governing equation
that describes the rate of change of 
, the measure variable, with time, as a function of , 
(time) and 
(some other measured variables). It is often not clear (a) whether the correct variables are considered, and (b) what the dynamic system, f, is. Instead, we can find ways to transform the unknown governing equation, given measured data, into
And typically, x(t) can be approximated in the form of an eigenvalue problem.
with solutions for x in the form of
where 
are the eigenfunctions, and 
are the eigenvalues.
The measured variables are often available as massive amounts of data measured for a long time. Say, the temperature distribution of a heated surface, , can be measured using an infrared camera with a resolution of 1000 x 1000 pixels and a acquisition frequency of 100 Hz. The time series of the dataset after m timesteps, can be represented as a 1E6 x m matrix. Let 
be the time series matrix of 
from j=1 to m-1, and 
be from j=2 to m.
There are many matrix A that predicts X from X’
One method of finding A is by defining a pseudoinverse (Moore-Penrose inverse), X+, such that,
a least squares solution for A can be found. However, the typically gigantuous size of X, and X’ can make solving for A unnecessarily difficult. Instead, applying a low-rank approximation is often sufficient. This can be done using the Singular Value Decomposition (SVD). The steps to shrink a large X to rank r, find the eigenvalues and eigenfunctions, then apply DMD is as follows:
- Apply SVD to X, apply rank-r truncation:
- Find the A matrix for the reduced rank X,
- Solve the eigenvalue problem
where columns of W are eigenvectors, and the diagonal of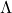
are the eigenvalues. - DMD mode (
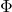) reconstruction
are the DMD modes. They are not necessarily orthogonal.
The originally measured variable x can then be reconstructed
One way to solve for b is by applying
to the above equation
While this version of DMD, the exact DMD, merely decomposes a high-rank time-varying experimental data, and does not explicitly reveal relationships between the measured (outcome) and controlled (input/intervened) variables, it provides insight to the dynamics of a complex system, extracting oscillating modes while respecting their time-dependence ( by the 
term).
My next step for this project is to (a) understand how this is different from a traditional Fourier transform, and (b) attempt to apply this method to a “relatively” low-rank experimental data set to better understand how the method works in practice (MATLAB).