The goal of this research is to find the spatial-temporal frequency components of a liquid film using DMD. The film thickness is measured using an optical technique, as shown in the schematic below. As a diffused laser propagates through the transparent window and the liquid film, beams reaching each interface with an incident angle greater than the critical angle are reflected completely due to total internal reflection. This occurs mostly at the vapor-liquid interface. Since the beams reflecting at this interface show the greatest intensity, the resulting image from the light source side of the transparent window resemble a light ring. A sample is shown below.
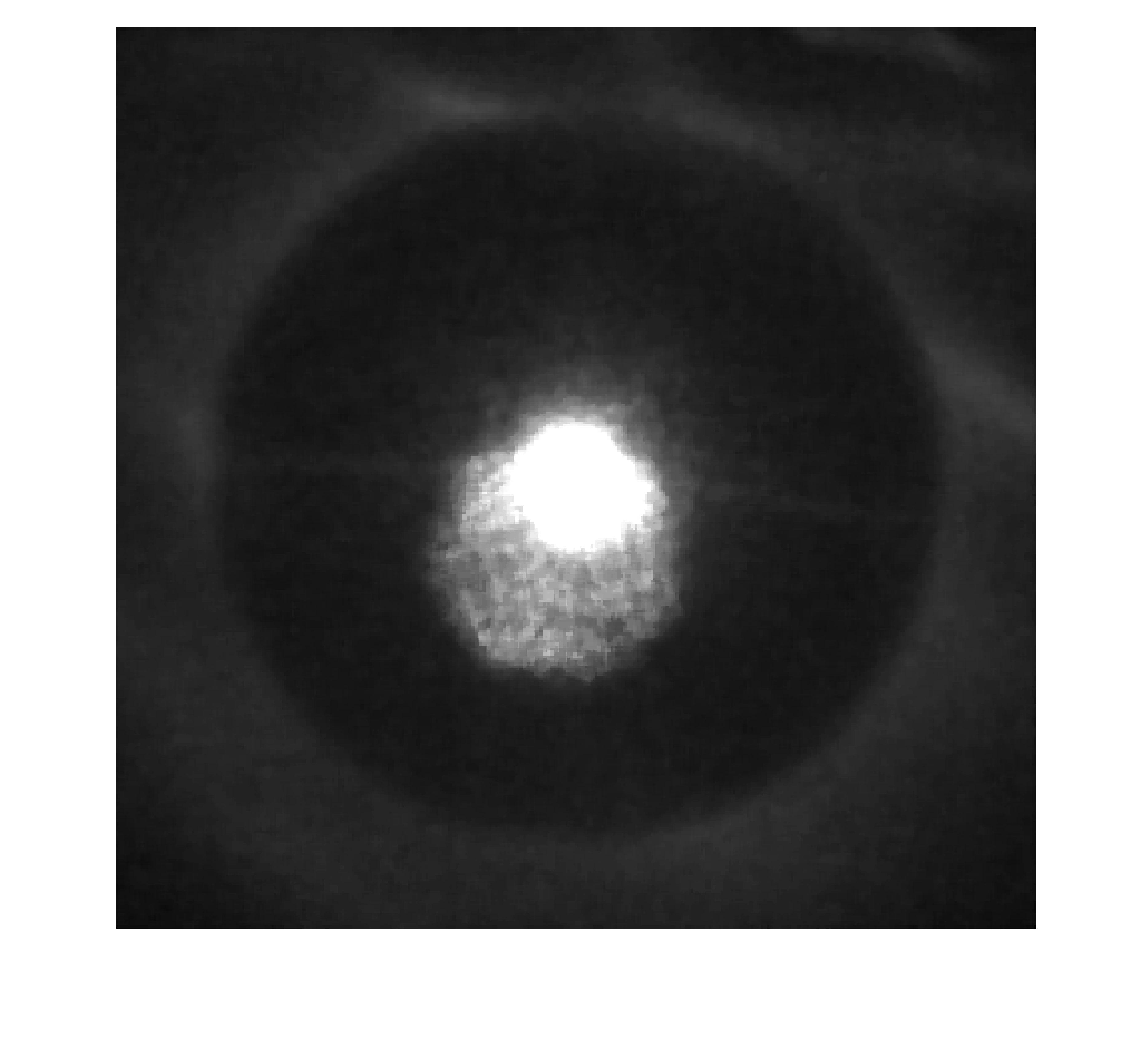
Originally, the inferred film thickness from the light ring images (as shown as time traces in the previous page) were used to perform DMD. However, due to the low spatial resolution (a single point in space), DMD was not able to identify modes in the data without employing a time-shift stacking technique to artificially pad the raw time trace signal.
Instead, the light ring images were used to show how the DMD algorithm works using MATLAB.
Simple DMD algorithm using MATLAB
% Sample DMD using Film Thickness Images
% Load data
data = load('results-all-14553899-12-Jul-2022.mat', 'th', 'fps');
dt = 1/data.fps; % Time step
t = (0:(length(th)-1)).*dt; % Time
% Load images
imPath = 'M:\Falling Film\Data\06232022\80g_30deg_2000fps';
im = imread(fullfile(imPath,sprintf('%06u.tif',1)));
imSize =size(im);
numIms = 4000;
% Read images data if not already done
if ~exist('X','var')
X = zeros(imSize(1)*imSize(2),numIms);
parfor idx = 1:numIms
im = imread(fullfile(imPath,sprintf('%06u.tif',idx)));
X(:,idx) = reshape(im,[],1);
end
end
% Create X1, X2
X1 = X(:,1:end-1);
X2 = X(:,2:end);
% SVD and rank-2 truncation
r = 30;
[U, S, V] = svd(X1, 'econ');
Ur = U(:, 1:r);
Sr = S(1:r, 1:r);
Vr = V(:, 1:r);
% Build Atilde and DMD Modes
Atilde = Ur' * X2 * Vr / Sr;
[W, D] = eig(Atilde);
Phi = X2 * Vr / Sr * W;
% DMD Spectra
lambda = diag(D);
omega = log(lambda)/dt
%% Plot
figure(4)
for plotIdx=1:20
subplot(4,5,plotIdx)
surf(flipud(abs(real(reshape(Phi(:,plotIdx),imSize(1),[]))))), shading interp, axis equal, view(2)
end
figure(5)
for plotIdx=1:20
subplot(4,5,plotIdx)
surf(flipud(abs(imag(reshape(Phi(:,plotIdx),imSize(1),[]))))), shading interp, axis equal, view(2)
end
The resulting mode shapes are shown in the images below.
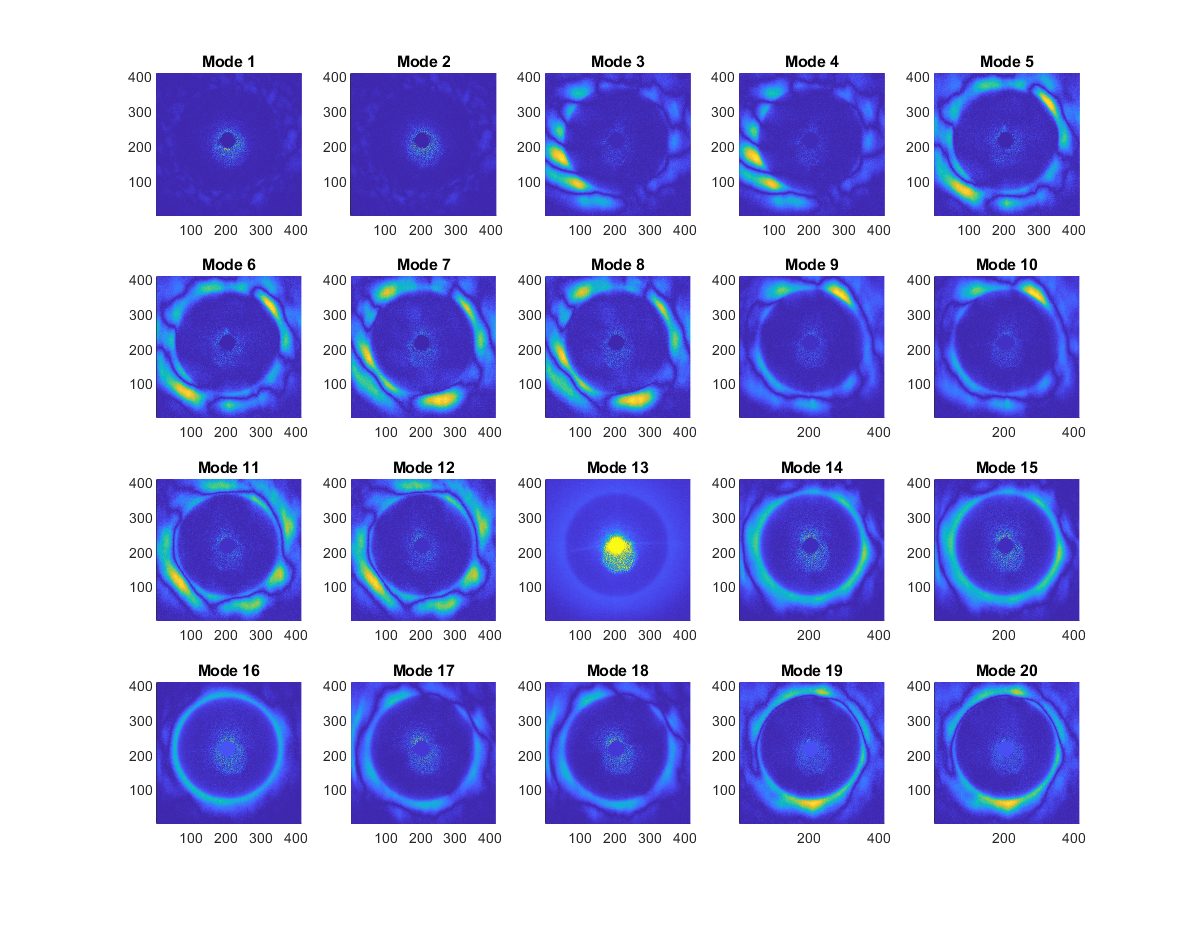
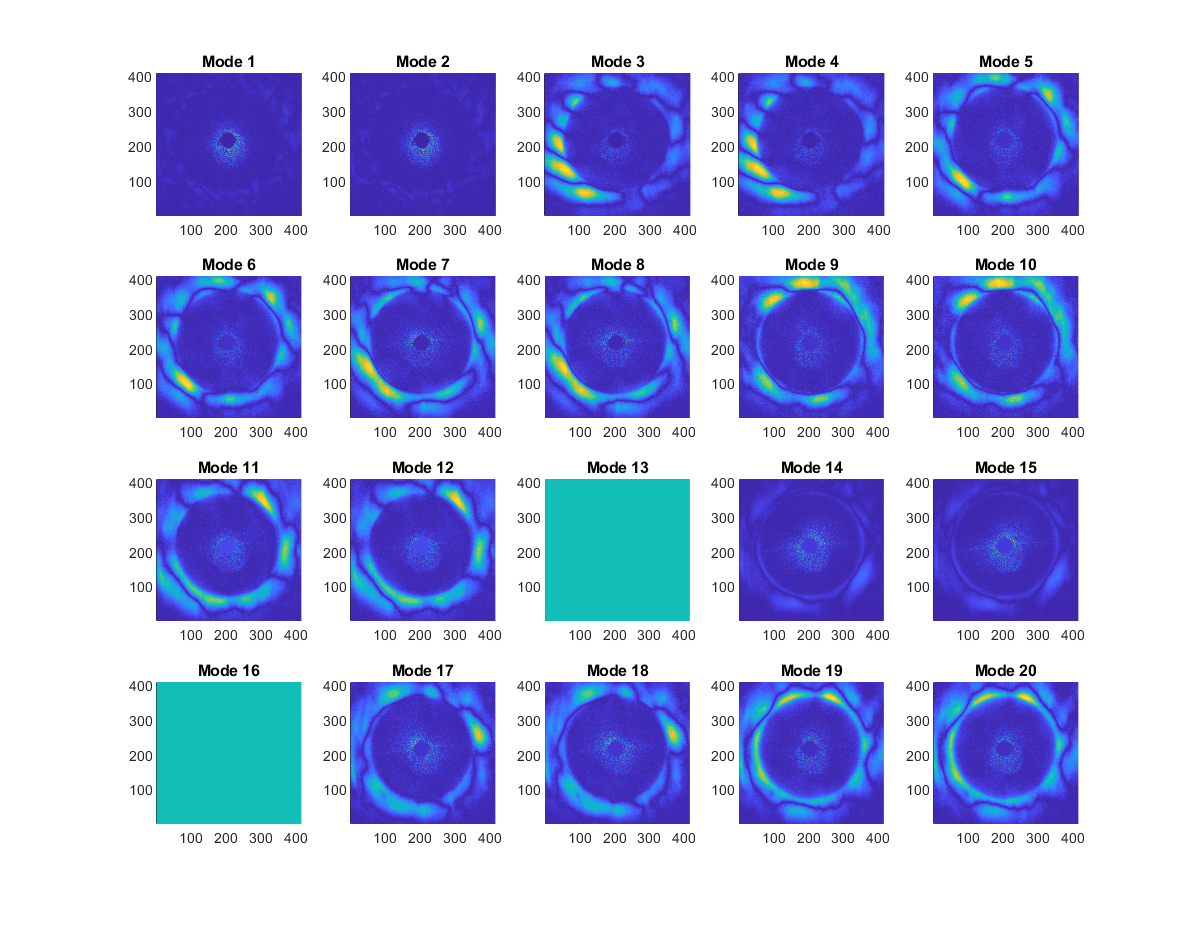
There are two main findings from these results:
- Unsuitable data for DMD
- While the light ring radii are directly proportional to the local film thickness, the intensity of the image areas radially outward from the rings captures the local film thickness gradient, but not the thickness itself. The DMD modes seem to be more sensitive to the changes in the ripples than the rings.
- For the goal of this task, collecting a 1-by-n vector of a ring radii (or film thickness through conversion) as a snapshot in time could be a more useful set of input data. This way, while the result of the DMD would not automatically generate a full 2D-map of the thickness within the ring, it should identify the modes of the ring, which can be useful in characterizing disturbance waves.
- On the other hand, direct flow images (i.e. images without the rings) can be used to identify frequency components of the wave, without measuring the film thickness. Both wave frequency (or velocity), and thickness are important in characterizing the mass flow rate of each wave. Current results already indicate that DMD modes of ripples can be identified.
- Insensitivity to translational and rotational invariance
- As demonstrated by Kutz et al. in Dynamic Mode Decomposition, rank-reduced normal DMD is insensitive to translational and rotational invariances in the data. Travelling disturbance waves in some film thickness or wave images are examples of such features.
- One of the best solutions to this insensitivity is the use of multi-resolution DMD, or mrDMD. mrDMD applies normal DMD recursively, decreasing the sampling time-window and retracting the low-rank order for each recursive layer. mrDMD is particularly suitable for image processing, and by extension surveillance video object detection, as it is well suited for object velocity and direction detection. The use of mrDMD will be demonstrated using direct images of falling film (no light ring) in the next section to investigate the sensitivity of the modified method on invariant features. The power spectra of DMD, mrDMD will also be compared with that of a discrete Fourier transform.